 Download BoyerMoore Class
Download BoyerMoore Class
 Download Speed-Comparison Project
Download Speed-Comparison Project
Introduction
NOTE: This article presents some code that the author does not recommend you use. Read on for more information.
The Boyer-Moore exact pattern matching algorithm is probably the fastest known algorithm for searching text that does not require an index on the text being searched. This algorithm works by creating a "skip table" to each possible character. Using this skip table, the number of actual comparisions needed to locate a string can decrease, in some cases dramatically.
Boyer-Moore Explained
As mentioned, Boyer-Moore uses a skip table that contains a skip value for all possible characters that may be encountered in the text being searched. This does require some preprocessing to build the table from the pattern being sought. Therefore, as a general rule, Boyer-Moore does not make sense where the text to search is small, or when there are multiple search patterns. But it does make sense where the text to search is large, or when there are multiple strings to be searched.
Let's examine the algorithm a little more closely. Consider the example where the search pattern is "ABC" and the text being searched is "ABXBABC", as shown in Figures 1 through 3.
One unique aspect of Boyer-Moore is that the comparison is done from right to left, starting with the last character in the pattern. Figure 1 shows the initial position where we start the comparison. In this example, the first comparison is between X and C, which do not match. But since X does not appear anywhere in the search pattern, we can now rule out a match anywhere in the first 3 characters. So the skip value for X will be initialized to 3, the length of the search pattern.
This example shows the advantage of starting the comparison from the right. It also shows why Boyer-Moore is fastest with long search patterns.
Figure 1: Mismatch with Character Not in Pattern
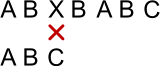
Figure 2 shows the position for the next comparison. Again we start from the right by comparing B and C, which again do not match. However, this time B does occur within the search pattern. The skip value for B will be 1 in order to line up with the last B in the search pattern.
Figure 2: Mismatch with Character in Pattern
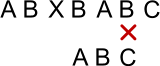
Figure 3 shows the position for the final comparison, where a match is found. In this trivial example, only 2 characters had to be compared prior to reaching this position.
Figure 3: Match Found

Working with Unicode Characters
Traditionally, implementations of this algorithm have created a 256-byte table to hold the skip value for all possible characters. However, .NET strings are Unicode and there are much more than 256 possible characters. (I don't know exactly how many. A double-byte value can accomodate 65,536 characters, but characters can consist of multiple "code points".)
So, when working with Unicode strings, you must either create a much larger table (where the exact size needed may be a little uncertain), or resort to other tricks. Given the memory available in modern computers, creating a larger table may be a valid choice. But I thought I'd experiment with a multi-stage table.
A multi-stage table has a master table, which then references other tables. The approach I used was to create a master array where each element references a byte array. Given a specific character, you can find the index into the master array by dividing the character value by the size of the array (in my code, 0x100). Once this element is found, you use the remainder of the division to find the index into the secondary table.
The vast majority of characters will not be in the search pattern, and the skip value for these characters will be the length of the pattern. Therefore, the first secondary array I create is one where all values are set to the length of the pattern. I then initialize all elements in the master array to reference this first secondary array.
Next, I go through and initialize skip values for characters that are in the pattern string. Where the corresponding entry in the master table still refers to the first secondary array, I create a new secondary array and have the master table reference the new array. The end result is that you end up with the master table and a couple of secondary tables. If the pattern string only contains regular English characters, they will all go into a single secondary table, resulting in the master table and two secondary tables.
The BoyerMoore Class
Listing 1 shows my BoyerMoore class. This listing also includes my UnicodeSkipArray class. The UnicodeSkipArray class implements multi-stage tables to reduce the amount of memory required for the skip table. It overrides the square brackets operator so that the class behaves just like a regular array.
The BoyerMoore class uses a simplified version of the algorithm and adds support for case-insensitive searches. For other variations of this algorithm, please see my speed comparision project, discussed below.
Listing 1: The BoyerMoore Class
/// <summary>
/// Implements a multi-stage byte array. Uses less memory than a byte
/// array large enough to hold an offset for each Unicode character.
/// </summary>
class UnicodeSkipArray
{
// Pattern length used for default byte value
private byte _patternLength;
// Default byte array (filled with default value)
private byte[] _default;
// Array to hold byte arrays
private byte[][] _skipTable;
// Size of each block
private const int BlockSize = 0x100;
/// <summary>
/// Initializes this UnicodeSkipTable instance
/// </summary>
/// <param name="patternLength">Length of BM pattern</param>
public UnicodeSkipArray(int patternLength)
{
// Default value (length of pattern being searched)
_patternLength = (byte)patternLength;
// Default table (filled with default value)
_default = new byte[BlockSize];
InitializeBlock(_default);
// Master table (array of arrays)
_skipTable = new byte[BlockSize][];
for (int i = 0; i < BlockSize; i++)
_skipTable[i] = _default;
}
/// <summary>
/// Sets/gets a value in the multi-stage tables.
/// </summary>
/// <param name="index"></param>
/// <returns></returns>
public byte this[int index]
{
get
{
// Return value
return _skipTable[index / BlockSize][index % BlockSize];
}
set
{
// Get array that contains value to set
int i = (index / BlockSize);
// Does it reference the default table?
if (_skipTable[i] == _default)
{
// Yes, value goes in a new table
_skipTable[i] = new byte[BlockSize];
InitializeBlock(_skipTable[i]);
}
// Set value
_skipTable[i][index % BlockSize] = value;
}
}
/// <summary>
/// Initializes a block to hold the current "nomatch" value.
/// </summary>
/// <param name="block">Block to be initialized</param>
private void InitializeBlock(byte[] block)
{
for (int i = 0; i < BlockSize; i++)
block[i] = _patternLength;
}
}
/// <summary>
/// Implements Boyer-Moore search algorithm
/// </summary>
class BoyerMoore
{
private string _pattern;
private bool _ignoreCase;
private UnicodeSkipArray _skipArray;
// Returned index when no match found
public const int InvalidIndex = -1;
public BoyerMoore(string pattern)
{
Initialize(pattern, false);
}
public BoyerMoore(string pattern, bool ignoreCase)
{
Initialize(pattern, ignoreCase);
}
/// <summary>
/// Initializes this instance to search a new pattern.
/// </summary>
/// <param name="pattern">Pattern to search for</param>
public void Initialize(string pattern)
{
Initialize(pattern, false);
}
/// <summary>
/// Initializes this instance to search a new pattern.
/// </summary>
/// <param name="pattern">Pattern to search for</param>
/// <param name="ignoreCase">If true, search is case-insensitive</param>
public void Initialize(string pattern, bool ignoreCase)
{
_pattern = pattern;
_ignoreCase = ignoreCase;
// Create multi-stage skip table
_skipArray = new UnicodeSkipArray(_pattern.Length);
// Initialize skip table for this pattern
if (_ignoreCase)
{
for (int i = 0; i < _pattern.Length - 1; i++)
{
_skipArray[Char.ToLower(_pattern[i])] = (byte)(_pattern.Length - i - 1);
_skipArray[Char.ToUpper(_pattern[i])] = (byte)(_pattern.Length - i - 1);
}
}
else
{
for (int i = 0; i < _pattern.Length - 1; i++)
_skipArray[_pattern[i]] = (byte)(_pattern.Length - i - 1);
}
}
/// <summary>
/// Searches for the current pattern within the given text
/// starting at the beginning.
/// </summary>
/// <param name="text"></param>
/// <returns></returns>
public int Search(string text)
{
return Search(text, 0);
}
/// <summary>
/// Searches for the current pattern within the given text
/// starting at the specified index.
/// </summary>
/// <param name="text">Text to search</param>
/// <param name="startIndex">Offset to begin search</param>
/// <returns></returns>
public int Search(string text, int startIndex)
{
int i = startIndex;
// Loop while there's still room for search term
while (i <= (text.Length - _pattern.Length))
{
// Look if we have a match at this position
int j = _pattern.Length - 1;
if (_ignoreCase)
{
while (j >= 0 && Char.ToUpper(_pattern[j]) == Char.ToUpper(text[i + j]))
j--;
}
else
{
while (j >= 0 && _pattern[j] == text[i + j])
j--;
}
if (j < 0)
{
// Match found
return i;
}
// Advance to next comparision
i += Math.Max(_skipArray[text[i + j]] - _pattern.Length + 1 + j, 1);
}
// No match found
return InvalidIndex;
}
}
Okay, So What's the Problem?
Okay, so the code in Listing 1 seems to work okay. Then why do I not recomend you use it? The problem is that it generally performs worse than String.IndexOf()!
In my initial tests, the BoyerMoore class was noticeably faster than String.IndexOf(), just as I had expected. However, I tried changing the code so that String.IndexOf() used the StringComparison.Ordinal comparison. After making that change, String.IndexOf() started outperforming the BoyerMoore class.
Calling String.IndexOf() with StringComparison.Ordinal allows a more direct comparison, which is basically what my BoyerMoore class does. I tested it with a couple of variations of the class, with and without the multi-stage tables and support for case-insensitive searches but String.IndexOf() was just faster. Performance characterstics of String.IndexOf() suggest that it does not use the Boyer-Moore algorithm. Instead, what appears to be happening is that it calls into unmanaged code that likely consists of hand-optimized assembly language. As a programmer writing managed C# code, it appears that I just can't compete with that.
The attached speed comparison project performs the tests I used if you'd like to experiment for yourself. It does not use the algorithm shown in Listing 1, which is a bit more flexible at the cost of some loss of performance.
Conclusion
So there you have it: An interesting search algorithm with an interesting way of using less memory to represent the skip table, and you're most likely better off just using String.IndexOf(). Of course, you could always implement your own hand-optimized assembly language to implement Boyer-Moore, but that's an article for another day.
End-User License
Use of this article and any related source code or other files is governed
by the terms and conditions of
.
Author Information
 Jonathan Wood
Jonathan Wood
I'm a software/website developer working out of the greater Salt Lake City area in Utah. I've developed many websites including Black Belt Coder, Insider Articles, and others.